2012年05月17日

コンプガチャだけじゃない!?　ガチャに潜む確率の罠

twitter をみていたら、こんなツイートが回ってきました。

モバゲー・GREEが確率明示しないのは、搾り取るためというよりは、クレーム対応減らすため。1％でSR、って書くと「100回引いたのに出ない。詐欺だ」。確率だから、って説明すると彼らはこう返す「だから、100回に1回出るんでしょ？」…さあ、どう返そうか。
— saintear/セインティアさん (@saintearRX) 5月 6, 2012

たしかに「1% のガチャを 100 回引いたら当たる」と思い込んでしまう人は多そうです。

では、1% のガチャを 100 回引くと、どれぐらいの人が当たり、どれぐらいの人が当たらないのでしょうか。

1% のガチャを 100 回引いて当たらない確率は？

さっそく計算してみましょう。

1 回ガチャを引いて当たらない確率は $\frac{99}{100}$ です。当たる確率は $1-\frac{99}{100}$ = 1% です。

2 回ガチャを引いたときに、1 度も当たらない確率は $\left(\frac{99}{100}\right)^2$ です。つまり、1 回以上当たる確率は $1-\left(\frac{99}{100}\right)^2$ = 1.9% となります。

3 回ガチャを引いたときに、1 度も当たらない確率は $\left(\frac{99}{100}\right)^3$ です。1 回以上当たる確率は $1-\left(\frac{99}{100}\right)^3$ で 2.7% です。

同じように計算していくと、結果はこうなります。

ケース	まったく当たらない確率	1 回以上当たる確率
1 回引いたとき	$\frac{99}{100}=99.0%$	1.0%
2 回引いたとき	$\left(\frac{99}{100}\right)^2=98.1%$	1.9%
3 回引いたとき	$\left(\frac{99}{100}\right)^3=97.3%$	2.7%
:	:	:
100 回引いたとき	$\left(\frac{99}{100}\right)^{100}=36.6%$	63.4%

1% のガチャを 100 回引いて 1 度も当たらない人は36.6%います。

当たらない人が意外に多いように感じませんか？

確率 1% は「100 回引けば必ず 1 回当たる」を意味するのではなく、「平均すると100 回に 1 回は出る」ことを意味します。100 回引いて 2 回も 3 回も当たる人がいる一方で、36.6% の人は 1 つも当たらずに終わってしまいます。

では、100 回以降も引き続けたとき、当たらない人の割合はどのように変わっていくのでしょうか。

グラフを描いてみました。

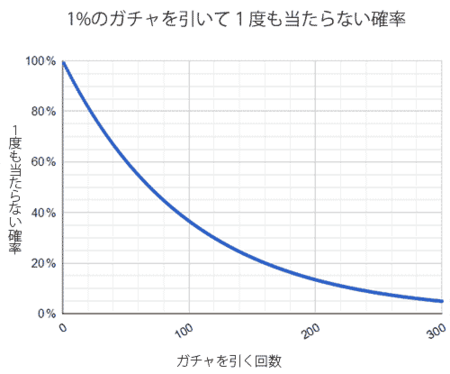
グラフから面白い性質が読み取れます。

1% のガチャを70 回ほど引いたところで半数の人は 1 度は当たる
1% のガチャを 100 回引いても 36.6% の人は当たりが出ない
1% のガチャを 200 回引いても 13.4% の人は当たりが出ない
1% のガチャを 300 回引いても 4.9% の人は当たりが出ない

20 人に1人は 300 回引いても当たりが出ません。これは恐怖です。

確率を変えて見えてくる 36% の不思議

ここまで、1% のガチャで調べてきましたが、ガチャの確率をいろいろ変えて計算してみましょう。

ケース	まったく当たらない確率	1 回以上当たる確率
20% のガチャを 5 回引いたとき	$\left(\frac{80}{100}\right)^5=32.8%$	67.2%
10% のガチャを 10 回引いたとき	$\left(\frac{90}{100}\right)^{10}=34.9%$	65.1%
5% のガチャを 20 回引いたとき	$\left(\frac{95}{100}\right)^{20}=35.8%$	64.1%
1% のガチャを 100 回引いたとき	$\left(\frac{99}{100}\right)^{100}=36.6%$	63.4%
0.5% のガチャを 200 回引いたとき	$\left(\frac{99.5}{100}\right)^{200}=36.7%$	63.3%
0.1% のガチャを 1000 回引いたとき	$\left(\frac{99.9}{100}\right)^{1000}=36.7%$	63.3%
0.01% のガチャを 10000 回引いたとき	$\left(\frac{99.99}{100}\right)^{10000}=36.8%$	63.2%

あれ？　ガチャの確率が 1% 以下だと、

まったく当たらない確率: 36.X%
1 回以上当たる確率: 63.X%

とほとんど同じ値です。

この不思議な性質は、パチンコをやる人には比較的知られている数字のようです。

この63%という数字はとても不思議な数字です。パチンコ台にはデジハネ（ハネデジと記載してい雑誌もあります）のように初当たり確率pが1/100前後の台から、エヴァンゲリオンのように1/400くらいの台まで様々な台がありますが、この数式で計算するとどんなスペックのパチンコ台でも1/p回転以内に初当たりが引ける確率は必ず63%になります。
パチンコのはまりと初当たり確率の関係:パチンコ、負けない立ち回りと確率の密接な関係

「36% の謎」。気になりますよね。高校数学を使って解き明かしてみましょう。

36% の謎を解く (高校3年生向け)

ここからは高校 3 年生の知識が必要になるので、少し難しくなります。（数学が苦手な人は飛ばしてください）

1% のガチャを 100 回引いて、一度も当たらない確率は $\left(1-\frac{1}{100}\right)^{100}$ です。

0.1% のガチャを 1000 回引いて、1度も当たらない確率は $\left(1-\frac{1}{1000}\right)^{1000}$ です。

これを一般化すると、次のようになります。

確率 1/n のガチャを n 回引く確率いて 1 度も当たらない確率は $\left(1-\frac{1}{n}\right)^{n}$

n を大きくしていったときの、

$\lim_{n\right\infty}\left(1-\frac{1}{n}\right)^{n}$

が求めたい値です。

ところで、指数関数 $e^x$ を原点で微分すると $\lim_{t\right0}\frac{e^t-1}{t}=1$ となります。ここに $t=\log\left(1+\frac{a}{n}\right)$ を代入すると、

$\lim_{n\right\infty}\left(1+\frac{a}{n}\right)^n=e^a$

という式を得ます。

この式に a = -1 を代入すると、

$\lim_{n\right\infty}\left(1-\frac{1}{n}\right)^{n}=\frac{1}{e}=0.367879...$

となります。

はい、以上で 36% の正体が分かりました。1 / e だったのです（e は自然対数の底 2.71828...)。

こんなところで、自然対数が出てくるのが不思議ですね。

同じ計算は複利計算にも応用できます。例えば、年利 1% で 100 年運用すると、資産はほぼ e 倍になります。

まとめ

「1% のガチャを 100 回引いても 36% の人は当たらない」ことが分かりました。

確率を変えて計算したところ、「1/n の確率のガチャを n 回引いても 36% の人は当たらない」(n≧100)という性質があることが分かりました。

この「36%」の罠は、パチンコにも存在します。パチンコとガチャが「36%」の罠でつながりました。

一方は法律で 18 歳未満は禁止されていて、ギャンブルであると世間では認知されていますが、もう一方は「ゲーム」であり、年齢制限はありません。

パチンコと似ているからといって、すぐに「賭博だ」「違法だ」とはなりません。「36%」の罠は、自然界や多くのゲームに潜んでいます。

ただ、最初に紹介した、

モバゲー・GREEが確率明示しないのは、搾り取るためというよりは、クレーム対応減らすため。1％でSR、って書くと「100回引いたのに出ない。詐欺だ」。確率だから、って説明すると彼らはこう返す「だから、100回に1回出るんでしょ？」…さあ、どう返そうか。
— saintear/セインティアさん (@saintearRX) 5月 6, 2012

というツイートは、ギャンブル慣れしていない大人や学生にギャンブル的なゲームを提供している状況を象徴しているように思えます。

※コンプガチャについても記事を書いていますので、興味のある方はどうぞ!!! → コンプガチャの確率マジックを中学生にも分かるように説明するよ