2012年05月11日

コンプガチャの確率マジックを中学生にも分かるように説明するよ

コンプガチャが話題になっています。

コンプガチャにハマりやすい理由として「最初は当たりやすいが、だんだん確率が低くなる」という指摘があります。

なぜ「確率が低くなる」という現象おきるのでしょうか。

この記事ではコンプガチャの裏側にある確率マジックを分かりやすく解説します。

サイコロの面を全部そろえるゲーム

いちばん身近な確率といえばサイコロです。

サイコロを使ったこんなゲームを考えてみます。

サイコロコンプのルール
サイコロを 1 回振るには 10 円が必要。
6 つの面をすべてを出せば、500ml のペットボトル飲料をプレゼント。

「サイコロの 6 つの面をすべてコンプしよう」というゲームなので、シンプルな「コンプガチャ」といえます。

このゲーム、あなたなら参加しますか？

6 つの面を全部だせばよいので、運がよければ 6 回（60円）でペットボトルが手に入ります。なんだかお得そうです。

ためしにやってみると・・・

サイコロを振ります。1投目。

はい、「6」が出ました。6 つの面のうち、1 つクリアです。

もう一度振ってみましょう。

「3」が出ました。6 つの面のうち、2 つクリアです。

第 3 投目。

今度は「2」です。

わずか 3 投で半分をコンプできました。なんだかとても楽勝なゲームに見えてきました。

厳しくなってくる後半戦

あと 3 回投げればコンプ成功しそうな気がしますか？

いやいや、ここからが難しくなってきます。6 つの面のうち、3 つは既に出たので、残りの 3 つの面を出さなければなりません。

1/2 の確率で失敗します。

サイコロだと、分かりやすいですよね。

だけど、実際のコンプガチャでは

「3千円で 3 枚出たんだから、8千円出せば 8 枚手に入る？」

と錯覚してしまいがちです。

こわいですね。

ゲームを続けていきましょう。第 4 投です。

あー、さっそく重複してしまいました。。。

第 5 投目。

「4」が出て、4 つクリアです。

ここからは 1/3 の確率になります。

すこし手間取って、9 投目にしてあと「1」が出ました。

残り 1 つです。

あと 1 個からの苦悩

ここまで 9 回投げて「5」は一度も出ていません。

9 回投げて「5」が出なかったんだから、次かその次には「5」が出てもよさそうです。

「もうそろそろ出てもいいだろう」と思ってしまうのが人間の心理です。

しかし、現実はそうではありません。確率の世界では、たとえ過去に 100 回連続で「5」が出てなくても、次に「5」が出る確率は 1/6です。中学では「同様に確からしい」という言葉を習ったのを覚えているでしょうか。あれです。（高校では、もうちょっと範囲を広げて「独立」という概念を習います）

確率が 1/6 ということは、平均すると 6 回投げないと当たりが出ません。運がよければ次に「5」が出るかもしれませんが、10 回投げても「5」が出でないかもしれません。100 回投げても出ないかもしれません。実際には何回投げるのかはやってみないと分からないけど、「平均すると 6 回投げる」ということです。

やめますか？

いや、ここでやめてしまうと 9 投目までに払った 90 円の投資はムダになってしまいます。

「次の 10 円で『5』がでるかもしれない」
「やめれば 90 円がムダになる」

という 2 つを比べると、やめると損するような気分になります。

やめられません。手を出してしまった以上、やめられないのがコンプガチャの怖さです。

意を決してサイコロを振り続けます。

出ません・・・。

16 投目でやっとでました。

16 投ということは 160 円です。ペットボトル飲料の定価 150 円を超えてしまいました・・・。

すべての結果をまとめると・・・

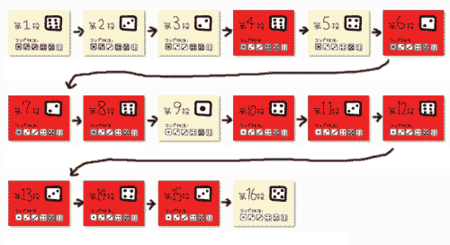
こうなりました。わずか 3 投目で半分までいったようにみえたのに、そのあと赤色が集中して、残りの 3 つをそろえるのに 13 回も投げる必要がありました。

「最初は簡単に当たるが、当たりが出るにつれて確率が下がる」ことが図をみて分かってもらえるのではないでしょうか。

いったい何回投げなきゃいけないの？

さて、では、このゲーム、平均でサイコロを何回投げればコンプできるのでしょうか。

一般に、

確率 p なら当たりがでるまで 1/p 回投げる必要がある

ことが分かっています。

なんのこっちゃ、と思うかもしれませんが、先ほど「確率 1/6 のときは 6 回投げる必要がある」と説明しました。p に 1/6 を当てはめれば、そのままですね。

ゲーム開始時点では、何が出ても当たりなので「当たる確率は 1」です。当然、1 つ当たるまでに投げる回数は 1 回です。

残りが 5 面のときは、最初に出たもの以外がでれば当たりなので「当たる確率は 5/6」です。2 つ目が当たるまでに投げる回数の期待値は 6/5 です。

同じように、整理していくと、こうなります。

残数	6	5	4	3	2	1
当たる確率	6/6	5/6	4/6	3/6	2/6	1/6
投げる回数の期待値	6/6	6/5	6/4	6/3	6/2	6/1

合計すると、投げる回数は

6/6 + 6/5 + 6/4 + 6/3 + 6/2 + 6/1 = 14.7 回

となります。

つまり、クリアまでに平均で 14.7 回投げる必要がある、ということです。

サイコロ面は 6 つなのに、すべて出すには 14.7 回も投げる必要があります。予想したよりも多いと感じませんか？

この記事ではザックリと計算しましたが、数学的に厳密な計算をしようとすると、無限級数の知識が必要だったり、期待値の線形性を理解している必要があったりします。

ちょうど同じ問題が数学ガール乱択アルゴリズム (数学ガールシリーズ 4) の 5 章で取り上げられています。この記事と同じぐらい丁寧に、この記事より厳密に解説してあるので、興味がある人は読んでみてください。本の中では、この問題のことを「確率の変化するコインを投げている」と表現していて、なるほど、と思いました。

数学ガール乱択アルゴリズム (数学ガールシリーズ 4)

作者: 結城浩
出版社/メーカー: ソフトバンククリエイティブ
発売日: 2011-03-02
メディア: 単行本
Amazon のレビューを見る

実際のコンプガチャはもっと複雑で低確率

実際のコンプガチャはもっと複雑です。

サイコロでたとえると

36 面あるサイコロのうち 1～10 をコンプしなきゃいけない
(コンプに無関係なアイテムが出る)
サイコロの重心がずれていて、特定の出目がでにくい（プレーヤーの間では、出にくいカードのことを「ストッパー」「門番」などと呼ぶそうです (2012/5/12 11:00 追記)）

といった状態です。

くわしく解説している記事によると、出現確率がバラバラなときにはコンプに必要な回数が増加するそうです。

等確率の設定よりもコンプに必要な回数は遙かに多くなる
出現確率のばらつきによってもコンプに必要な回数は変動する
300円ガチャであれば10種類のアイテム数でもコンプまでに10万円以上かかる設定が可能である
以下が主な数値結果。
# 3種類
(1/3, 1/3, 1/3) -> 5.5回
(1/6, 1/3, 1/2) -> 7.3回
(1/10, 4/10, 5/10) -> 10.7回
コンプガチャの数理 -コンプに必要な期待回数の計算方法について- - doryokujin's blog

まとめ

いかがだったでしょうか。

「コンプガチャ」といってしまうと確率のイメージが沸きにくいですが、「サイコロの面を全部そろえるゲーム」に置き換えることで、

最初は簡単にそろう
後半になると出にくくなり、心理的にも後に引けなくなる

ことが分かっていただけたでしょうか？

このような「サイコロの面を全部そろえたら商品がもらえる」というゲームは「カード合わせ」「絵合わせ」と呼ばれ、景品表示法で禁止されています。過去に「プロ野球チップス」が流行った 1977 年頃に社会問題になって禁止されたそうです。今回のコンプガチャ騒動では、コンプガチャが「カード合わせ」「絵合わせ」に当たるとして消費者庁が指摘した形になります。

この記事を書くにあたって、次の記事や本を参考にしました。

→ (追記) 続編を書きました コンプガチャだけじゃない!?　ガチャに潜む確率の罠