詳解 ActionScript 3.0アニメーション ―衝突判定・AI・3DからピクセルシェーダまでFlash上級テクニック を読んでいて、経路探索のアルゴリズムで A* が取り上げられていました。

A* については、いろいろ検索して調べたりもしたのですが、やっぱり本に書いてあると理解しやすいですね。せっかくなので自分流に実装してビジュアライズしてみました。

ダイクストラ法

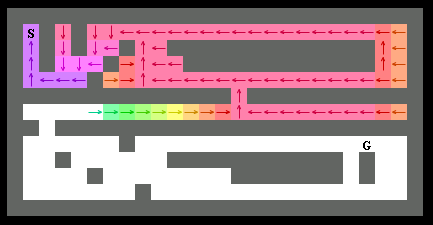
まずは A* の特別なケースでもあるダイクストラ法から見ていきます。クリックすると探索のシミュレーションが開始します。

スタート地点(S)からゴール(G)への探索が始まります。

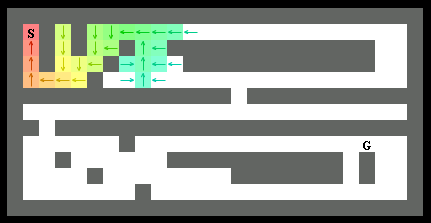
色がついたところが「最短経路が決定した場所」です。スタート地点から少しずつ探索が完了していきます。

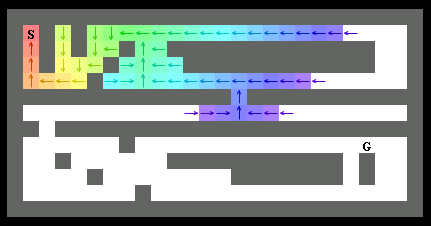
半分ぐらい完了しました。まだまだ進みます。

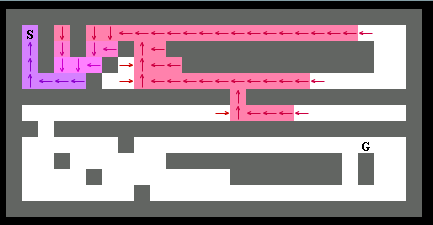
最後まで終わりました。最短経路を黒色矢印で表示しています。

ダイクストラ法は、スタート地点から近いノード(=マス目)から順番に最短経路が判明していきます。

ざっくりとした例えですが、スタート地点から水をたらして広がった順番に経路が決定していくようなイメージです。水は均等に広がっていくので、一番最初に到達した水滴について、たどってきた道を確認すれば経路が判明するわけです。

A*(A-Star)

次に A* の探索過程を見てみましょう。大枠はダイクストラ法と同じなのですが、探索の道順が異なります。

A* ではゴールへの距離が近いノードを優先的に調べていきます。右方向のノードを調べにいってますね。

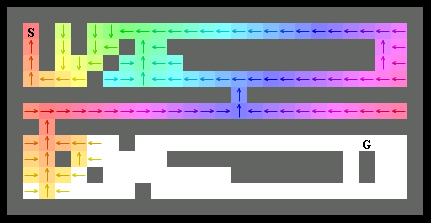
上半分を探索し終わったら、仕方なくゴールから遠ざかる左方向に移動していきます。

そのあとはゴールに向かって一直線です。

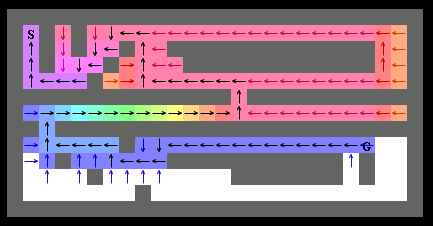
A* ではゴールへの経路が判明した段階で処理は終了です。

A* はダイクストラ法に比べてゴールに到達するまでに調べるマス目が少ないのが印象的です。

ダイクストラ法と同じように水で例えると、A* では水が少し意思を持っていて、なるべくゴールに近いほうに流れようとするようなイメージです。ここがまさに A* のキモです。ゴールへの近さを加味して、探索するノードの数をなるべく減らそうとします。

A* では、スコアとして f* = g* + h* を用います。各ノードの f* を調べて、f* の値が小さいノードから先に探索していきます。g* はスタート地点からの距離であり、ダイクストラ法で用いるスコアと同じです。h* がゴールへの距離なのですが、実際の最短距離は途中の段階では分からないので、ゴールへの直線距離やマンハッタン距離を利用して計算します。

この、h* の部分がゴールへの近さを加味する部分です。スタートからの距離が同じノードが複数ある場合には、h*(=ゴールへの距離)が近いものから調べていこう、という作戦です。

もし、h* が 0 ならダイクストラ法と同じ処理になります。h* が実際の最短距離より小さい値である限りは、選んだノードが最短距離であることが保証されているようです。直線距離やマンハッタン距離を使ってる限りは、それよりも最短距離が小さくなることはありませんね。

まとめ

ダイクストラ法と A* の探索途中の様子をビジュアライズしてみました。

ソースコードは wonderfl に投稿しています（ダイクストラ法・A*）。それぞれ200行ほどですがコメントはしっかり書いたつもりですし、ソースの diff は40行ほどなので共通点も多いです。よければ参考にしてください。

ちなみに、私が参考にした 詳解 ActionScript 3.0アニメーション のデモは、O'REILLY のサイト から閲覧できますし、ソースコードも ダウンロードできます。太っ腹！

詳解 ActionScript 3.0アニメーション ―衝突判定・AI・3DからピクセルシェーダまでFlash上級テクニック

• 作者: Keith Peters
• 出版社/メーカー: オライリージャパン
• 発売日: 2010-01-25
• メディア: 大型本
• Amazon のレビューを見る