クラスタリングの定番アルゴリズム「K-means法」をビジュアライズしてみた
集合知プログラミング を読んでいたら、K-means 法(K平均法)の説明が出てきました。
K-means 法はクラスタリングを行うための定番のアルゴリズムらしいです。存在は知っていたんだけどいまいちピンときていなかったので、動作を理解するためにサンプルを作ってみました。
クリックすると1ステップずつ動かすことができます。クラスタの数や点の数を変更して、Restart を押すと好きなパラメータで試すことができます。
こうやって1ステップずつ確認しながら動かしてみると、意外に単純な仕組みなのが実感できました。
(追記) HTML5 版の K-means 法を D3.js でビジュアライズしてみた も作成しました。Flash を表示できない環境ではそちらをご覧ください。
K-means 法とは
K平均法 - Wikipedia に詳しく書いてあるけど、もうすこしザックリと書くとこんなイメージになります。
- 各点にランダムにクラスタを割り当てる
- クラスタの重心を計算する。
- 点のクラスタを、一番近い重心のクラスタに変更する
- 変化がなければ終了。変化がある限りは 2. に戻る。
これでも分かりにくいですね。例題を紹介しましょう。
図で解説!
(ステップ1) 1. 初期状態
これが初期状態です。色がクラスタを表していています。5色あるので、クラスタは5つですね。
各点にランダムな色を割り振っています。

(ステップ2) 2. 重心を計算する
クラスタごとに重心(座標の平均値)を求めます。×印が重心です。

(ステップ3) 3. 一番近い重心の色に変わる
それぞれの点の色を塗り替えます。自分から一番近い重心の色に変わります。

青の重心は近くに点が少ないので、寂しいクラスタになっちゃってますね。
(ステップ4) 2. 再度、重心を計算する
重心の位置やクラスタに変化があったので、2. に戻ります。
新しいクラスタでの重心の位置を求めます。×印がクラスタの中心に移動してますね。

(ステップ5) 3. 再度、色を置き換える
新しい重心の位置に応じて、もう一度色を置き換えます。青と黄が勢力を拡大しました。
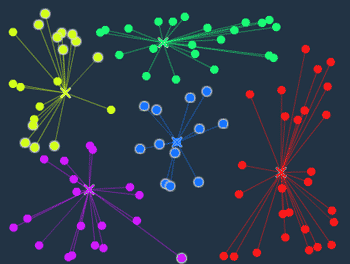
(ステップ6) 2. また重心を計算する
相変わらず変化があったので、重心の位置をもう1度計算します。
黄緑の重心が少し右方向に移動しました。
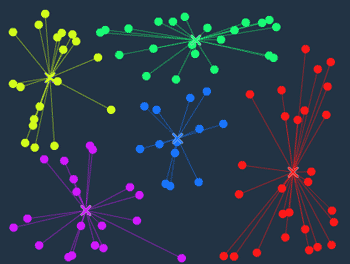
(ステップ7) 3. また色を置き換える
再クラスタリングします。
黄緑が赤を少し奪い、黄色が黄緑を少し奪いました。
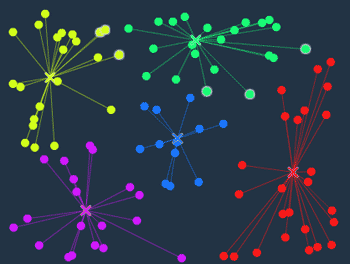
(ステップ7) 2. またまた重心を計算する
黄緑の重心が、さらに右に移動しました。
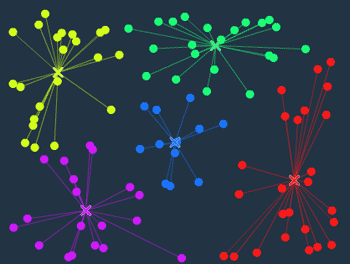
(ステップ8) 3. またまた色を置き換える
黄緑がさらに右方向に勢力を拡大しています。それに伴い、左の方の陣地は、黄色や青色に奪われています。
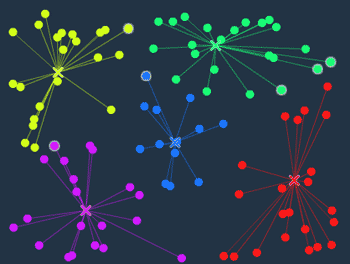
(最後) 9. 変化がなくなった
さらに何ステップか経過させた結果、ここで終了しました。

最終的に黄緑は右上の点を占領したようです。
全ての点が一番近い重心に属していて、重心の位置も変化しない状態です。それらしく色分けできているのが分かります。
まとめ
K-means 法は単純な仕組みで動いていることが分かりました。単純だからこそ、色んな改良をしやすいんでしょうね。
ソースコードは少し長いので http://tech.nitoyon.com/misc/swf/KMeans.as に置いています。

- 作者: Toby Segaran
- 出版社/メーカー: オライリージャパン
- 発売日: 2008-07-25
- メディア: 大型本
- Amazon のレビューを見る