AS3.0 で 3D プログラミングを1から勉強する (4) - 面に色を塗る
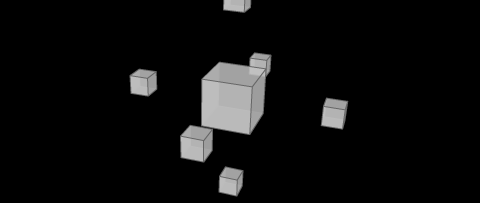
ワイヤーフレームにも飽きてきたので、色を塗ることにしよう。面に色を塗ることを、3D 用語ではシェーディングと呼ぶらしい。今回はその中でもシンプルなフラットシェーディングという技法を取り上げる。
といっても、ActionScriptによるWebの3Dグラフィックス再入門 (2) - シェーディングでもっと3Dらしく:CodeZine で解説されてる通りにコーディングしているので、詳しいことはそちらの記事に譲ろう。
コーディング結果はこうなった。
だいぶ嬉しい感じ。
これで終わるのもさすがに寂しいので、ソースの全体の流れを説明しておこう。
- 奥の立方体から描画するために並べ替える
- 立方体の面についても奥の面から描画するために並べ替える
- 各面の法線ベクトルを求める
- 面の明るさを求める
- 面を描画する
それぞれについて簡単にみていく。
1. 奥の立方体から描画するために並べ替える
面を塗るにあたっては、塗る順番が重要になる。先に手前の物体を描いてしまうと、奥の物体が上に描画されてしまう。
そこで、奥のものから順番に塗る必要がある。ここでは一番手軽な Z ソートという手法を使う。立派な名前がついてるが、何のことはない、奥の面から順番に塗っていく手法のことである。
今回のソースでは、まずは立方体ごとに塗る順番を決めることにした。Cube クラスに center プロパティを導入して、Z 座標が大きい(奥のもの)から順番に描画している。
// 回転行列を作成
var matrix:Matrix3D = new Matrix3D();
matrix.rotateX(Math.PI / 6);
matrix.rotateY(rad / 180 * Math.PI * 3);
matrix.rotateZ(rad / 180 * Math.PI);
// それぞれの立方体の中心のZ座標を取得する
var dic:Dictionary = new Dictionary();
for each(var c:Cube in cubes){
var center:Point3D = matrix.transformPoint(c.center);
dic[c] = center.z;
}
// Zソート (奥のものから順番に並べる)
cubes.sort(function(a:Cube, b:Cube):Number {
return dic[b] - dic[a];
});
// 奥から描画
for each(c in cubes){
c.draw(canvas.graphics, matrix, 200);
}
Zソートは簡単な分、入り組んだ物体や面が交差するような場合には使えない。そういう複雑な物体を描画するときにどうするかはまだよく分かってない。
2. 立方体の面についても奥の面から描画するために並べ替える
立方体のそれぞれの面についても、奥の面から順番に描画していく。手順は 1. と同じなので省略。
3. 各面の法線ベクトルを求める
ここからは面の色を求める作業が始まる。まずは、面の法線ベクトルを求める。法線ベクトルというのは、面に垂直なベクトルのこと。
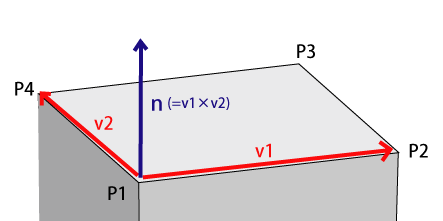
まず、面の2辺を表すベクトル v1 と v2 を求める。Point3D のベクトルの差を求めるメソッド subtract を利用している。
var v1:Point3D = p2.subtract(p1); var v2:Point3D = p4.subtract(p1);
次に v1 と v2 の外積を計算する。外積は2つのベクトルに垂直なベクトルとなる。
var n:Point3D = cross(v1, v2);
外積を計算する関数は Point3D に用意されていなかったので自前で作った。
// 外積
function cross(p1:Point3D, p2:Point3D):Point3D {
return new Point3D(p1.y * p2.z - p1.z * p2.y,
p1.z * p2.x - p1.x * p2.z,
p1.x * p2.y - p1.y * p2.x);
}
あと、外積は順番が大事なのでそこに気をつけるべし。v1×v2 は立方体の外側に向かうベクトルだが、v2×v1だと内側に向かうベクトルになってしまう。
最後に、n を単位ベクトル(長さ1のベクトル)にしておこう。
n.normalize(1);
normalize() は Poitn3D に定義されているものをそのまま活用した。
4. 面の明るさを求める
光源の方向を表すベクトルを l とする。
var l:Point3D = new Point3D(0, 0, -1);
l と n の内積を面の明るさとする(ランバートの法則というらしい)。
l も n も単位ベクトルのため、
l・n = |l||n|cosθ = cosθ (θはlとnの間の角度)
となる。つまり、l と n が同じ向きのときに最も明るくなる。
5. 面を描画する
明るさが求まれば、あとは色を求めて塗るだけ。
var product:Number = n.dot(l); var b:int = 0x3f * product + 0xc0; g.beginFill(b * 0x10000 + b * 0x100 + b, 0.6);
まとめ
面を塗ると 3D っぽくなる。幸せ。
あと、id:rch850 さんは早く ActionScriptによるWebの3Dグラフィックス再入門:CodeZine の第3回を執筆すべき。
ソースコードは以下に(157行)。
要 FIVe3D 2.1 の five3d.geom.Matrix3D クラスと five3d.geom.Point3D クラス。
package {
import flash.display.*;
import flash.utils.Dictionary;
import five3D.geom.Matrix3D;
import five3D.geom.Point3D;
[SWF(backgroundColor="0x000000")]
public class Study3d4 extends Sprite{
private var canvas:Sprite;
private var cubes:Array;
private var rad:Number;
public function Study3d4(){
stage.scaleMode = "noScale";
stage.align = "TL";
cubes = [];
cubes.push(new Cube(0, 0, 0, 50));
cubes.push(new Cube(0, 100, 0, 20));
cubes.push(new Cube(0, -100, 0, 20));
cubes.push(new Cube(100, 0, 0, 20));
cubes.push(new Cube(-100, 0, 0, 20));
cubes.push(new Cube(0, 0, 100, 20));
cubes.push(new Cube(0, 0, -100, 20));
canvas = new Sprite();
addChild(canvas);
canvas.x = 200;
canvas.y = 150;
rad = 0;
changeHandler(null);
addEventListener("enterFrame", changeHandler);
}
private function changeHandler(event:Object):void {
canvas.graphics.clear();
// 回転行列を作成
var matrix:Matrix3D = new Matrix3D();
matrix.rotateX(Math.PI / 6);
matrix.rotateY(rad / 180 * Math.PI * 3);
matrix.rotateZ(rad / 180 * Math.PI);
// それぞれの立方体の中心のZ座標を取得する
var dic:Dictionary = new Dictionary();
for each(var c:Cube in cubes){
var center:Point3D = matrix.transformPoint(c.center);
dic[c] = center.z;
}
// Zソート (奥のものから順番に並べる)
cubes.sort(function(a:Cube, b:Cube):Number {
return dic[b] - dic[a];
});
// 奥から描画
for each(c in cubes){
c.draw(canvas.graphics, matrix, 200);
}
// 角度更新
rad = (rad + 1) % 360;
}
}
}
import flash.display.Graphics;
import flash.geom.Point;
import flash.utils.Dictionary;
import five3D.geom.Point3D;
import five3D.geom.Matrix3D;
class Cube {
private var points:Array = [];
private var _center:Point3D;
public function get center():Point3D {
return _center;
}
public function Cube(x:Number, y:Number, z:Number, len:Number){
_center = new Point3D(x, y, z);
var diff:Function = function(f:Boolean):Number{return f ? len / 2 : -len / 2;};
// 立方体の頂点8つを作成する
for(var i:int = 0; i < 8; i++){
var p:Point3D = new Point3D(x + diff(i % 4 % 3 == 0), y + diff(i % 4 < 2), z + diff(i < 4));
points.push(p);
}
}
public function draw(g:Graphics, matrix:Matrix3D, f:Number):void {
// 回転後の座標を計算
var p:Array = [];
for(var i:int = 0; i < points.length; i++){
var pt:Point3D = matrix.transformPoint(points[i]);
p.push(pt);
}
// 面の一覧
var planes:Array = [
[p[0], p[1], p[2], p[3]],
[p[7], p[6], p[5], p[4]],
[p[0], p[4], p[5], p[1]],
[p[1], p[5], p[6], p[2]],
[p[2], p[6], p[7], p[3]],
[p[3], p[7], p[4], p[0]]
];
// 面の中心のZ座標を求める
var z:Dictionary = new Dictionary();
for(i = 0; i < planes.length; i++){
z[planes[i]] = (planes[i][0].z + planes[i][1].z + planes[i][2].z + planes[i][3].z) / 4;
}
// Zソート (奥のものから順番に並べる)
planes.sort(function(a:Array, b:Array):Number {
return z[b] - z[a];
});
// 奥から順番に面を描画
for each(var plane:Array in planes){
drawPlane(g, plane[0], plane[1], plane[2], plane[3]);
}
}
private function drawPlane(g:Graphics, p1:Point3D, p2:Point3D, p3:Point3D, p4:Point3D):void {
// 単位法線ベクトル
var v1:Point3D = p2.subtract(p1);
var v2:Point3D = p4.subtract(p1);
var n:Point3D = cross(v1, v2);
n.normalize(1);
// 光源の方向ベクトルとの内積
var l:Point3D = new Point3D(0, 0, -1);
var product:Number = n.dot(l);
// 透視投影しつつ面を塗る
var b:int = 0x3f * product + 0xc0;
g.beginFill(b * 0x10000 + b * 0x100 + b, 0.6);
g.lineStyle(0, 0x666666);
var p:Point3D;
p = p1.clone(); p.project(p.getPerspective(500)); g.moveTo(p.x, p.y);
p = p2.clone(); p.project(p.getPerspective(500)); g.lineTo(p.x, p.y);
p = p3.clone(); p.project(p.getPerspective(500)); g.lineTo(p.x, p.y);
p = p4.clone(); p.project(p.getPerspective(500)); g.lineTo(p.x, p.y);
g.endFill();
}
}
// 外積
function cross(p1:Point3D, p2:Point3D):Point3D {
return new Point3D(p1.y * p2.z - p1.z * p2.y,
p1.z * p2.x - p1.x * p2.z,
p1.x * p2.y - p1.y * p2.x);
}