3D の原理をあまり知らなかったので、ActionScript 3.0 で１から勉強してみた。１からなのでフレームワークは使わず、自力で実装していく。

Web 上には色んな資料があってありがたいだけど、玉石混交な上に、有用なものでも一本道で幅の狭いものが多い。前提知識のない自分にとっては、資料間の関連性を理解するのが大変だった。

なので、なるべく簡単なところからスタートしつつ、広く浅く体験していくことを目標としてみる。まずは、四面体をワイヤーフレームで表示するところからスタートしよう。

四面体を定義する

まずは、3次元上の点を表現する Point3D クラスを作る。

class Point3D {
    public var x:Number;
    public var y:Number;
    public var z:Number;

    public function Point3D(_x:Number = 0, _y:Number = 0, _z:Number = 0){
        x = _x;
        y = _y;
        z = _z;
    }
}

四面体を作るために、メインのクラスに４つの点を定義した。

public class Study3d1 extends Sprite{
    private var p1:Point3D = new Point3D(  0,   0, 100);
    private var p2:Point3D = new Point3D(100,   0,   0);
    private var p3:Point3D = new Point3D(  0, 100,   0);
    private var p4:Point3D = new Point3D(-50, -50, -50);

２次元空間に表示する

３次元の点を２次元空間に描画する方法を考える。

とはいえ、一番最初のサンプルなので、真上（もしくは真下）から見たところを表示する。つまり、Z の値を無視して表示する。３次元空間上の(0, 0, 100) という点は、(0, 0) に表示する。

プロット先の座標を求めて（といっても、Zの値を無視するだけだけど）、線で結んでやれば四面体を真上から見た図ができた。

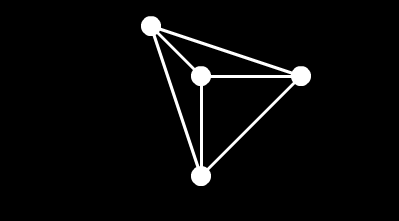
回転！

これだとあまりにも退屈なので、回転させてみよう。

カメラが回転するのは難しいので、四面体に回転してもらうことにする。こっちはちょー簡単。

ある点 p を原点周りに rad ラジアンだけ回転させるには

p.x =  Math.cos(rad) * x + Math.sin(rad) * y;
p.y = -Math.sin(rad) * x + Math.cos(rad) * y;

とする。(詳しく知りたい人は「回転行列」あたりのキーワードで検索すべし)

x と y を y と z に置き換えれば X 軸周りの回転になるし、z と x に置き換えれば Y 軸周りの回転になる。

マウスの位置に応じて Y 軸周りと Z 軸の周りに回転させるようにしてみた。回転後の座標を線で繋げば回転する四面体の完成だ。

ソースはたった86行。ローテクだけど、回転し続けていれば立体に見えなくもない。

第２回に続く。

今回のソースは以下に（86行）。

package {
    import flash.display.*;
    import flash.geom.Point;

    [SWF(backgroundColor="0x000000")]
    public class Study3d1 extends Sprite{
        private var p1:Point3D = new Point3D(  0,   0, 100);
        private var p2:Point3D = new Point3D(100,   0,   0);
        private var p3:Point3D = new Point3D(  0, 100,   0);
        private var p4:Point3D = new Point3D(-50, -50, -50);

        private var canvas:Sprite = new Sprite();

        public function Study3d1(){
            stage.scaleMode = "noScale";
            stage.align = "TL";

            addChild(canvas);
            canvas.x = 150;
            canvas.y = 150;

            changeHandler(null);
            addEventListener("enterFrame", changeHandler);
        }

        private function changeHandler(event:Object):void {
            var pp1:Point3D = rotate(p1);
            var pp2:Point3D = rotate(p2);
            var pp3:Point3D = rotate(p3);
            var pp4:Point3D = rotate(p4);

            canvas.graphics.clear();
            drawPoint(pp1); drawPoint(pp2);
            drawPoint(pp3); drawPoint(pp4);
            drawLine(pp1, pp2); drawLine(pp1, pp3); drawLine(pp1, pp4);
            drawLine(pp2, pp3); drawLine(pp2, pp4); drawLine(pp3, pp4);
        }

        private function drawPoint(p:Point3D):void {
            canvas.graphics.beginFill(0xffffff);
            canvas.graphics.drawCircle(p.x, p.y, 10);
            canvas.graphics.endFill();
        }

        private function drawLine(p1:Point3D, p2:Point3D):void {
            canvas.graphics.lineStyle(3, 0xffffff);
            canvas.graphics.moveTo(p1.x, p1.y);
            canvas.graphics.lineTo(p2.x, p2.y);
            canvas.graphics.lineStyle();
        }

        private function rotate(_p:Point3D):Point3D {
            var ret:Point3D = new Point3D(_p.x, _p.y, _p.z);
            var p:Point;

            // y rotate
            p = rotate2d(ret.z, ret.x, stage.mouseX / 180 * Math.PI);
            ret.z = p.x; ret.x = p.y;

            // z rotate
            p = rotate2d(ret.x, ret.y, -stage.mouseY / 180 * Math.PI);
            ret.x = p.x; ret.y = p.y;

            return ret;
        }

        private function rotate2d(x:Number, y:Number, rad:Number):Point {
            var p:Point = new Point();
            p.x =  Math.cos(rad) * x + Math.sin(rad) * y;
            p.y = -Math.sin(rad) * x + Math.cos(rad) * y;
            return p;
        }
    }
}

class Point3D {
    public var x:Number;
    public var y:Number;
    public var z:Number;

    public function Point3D(_x:Number = 0, _y:Number = 0, _z:Number = 0){
        x = _x;
        y = _y;
        z = _z;
    }
}