2007年09月19日

ベジエ曲線の仕組み (2) - ２次ベジエ曲線を詳しく

前回の種明かしをする前に、ベジエ曲線の定義を見てみてみましょう。

ベジエ曲線の定義

２次ベジエ曲線は３つの制御点から成り立っています。制御点から曲線を求めるには次のようにします。

制御点を t : 1 - t (0≦t≦1) に内分する点を結んで直線を引く。（上の図で常時動いている直線になる）
この直線を t : 1 - t に結んだ点を求める（上の図の黒い点）。

上の図で青い残像になっている部分が２次ベジエ曲線になります。

前回の図と比較

では、前回の図と比較してみましょう。

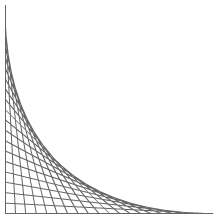
図2

直感的に「ベジエ曲線だ！」と言いたくなってしまいますが、そう早まってはいけません。この曲線がベジエ曲線から少しでもずれていれば、ベジエ曲線とはいえません。

「ベジエ曲線だよ！」と言い切るためには数学の力を借りる必要があります。センター試験の文型数学レベルの内容なので、よかったら読んでみてください。

証明１：力技

証明1 図のように、３つの制御点をそれぞれ (0, 0), (1, 0), (0, 1) としておきます。この座標で証明できれば、拡大縮小したり歪ませた座標系でも同じように証明できます。

直線を表す方程式を $y = f(x)$ とすると、(0, 1 - t) と (t, 0) を通るという条件から、 $f(x) = -(\frac{1}{t}-1)x + 1 - t$ と求められます。

さて、x 座標が $x_0$ である点に着目します。

この点の座標は $(x_0, f(x_0)$ です。t を変数として考えると、t の値によって y座標の値は変化します。

つまり、

$\Large\left.\begin{eqnarray} f(t) &=& -(\frac{1}{t}-1)x_0 + 1 - t\\ &=& -t - \frac{x_0}{t} + x_0 + 1 \end{eqnarray}\right\.$

となります。

f(t) が最大値をとるとき、点 $(x_0, f(t))$ は図2の曲線を構成する点になります。

ここまでくればあとは計算するだけ。f(t) を微分すれば、 $t = \Large\sqrt{x_0}$ のとき f(t) が最大値になることが分かります。

ここから、 $x_0 : t = t^2 : t = t : 1$ となることが分かります。つまり、ベジエ曲線は t : 1 - t を満たす点(図1の黒丸)の集合なのだけど、それは図2において y 座標を最大にする点の集合と同じなのです。

おわり。

証明２：ちょっとエレガントに

証明2 証明１は力技だったのであまり美しくありません。もうちょっとエレガントに回答すると、証明も短くなりますし、物事の本質も見えてくるものです。

ということで、さっきの図を45度傾けて計算してみます。制御点は原点と(1, 1), (-1, 1) です。

ベジエ曲線を表す式を求めます。t : 1 - t に内分した点は (t, t)、(t - 1, 1 - t) となります。この２点を t : 1 - t に内分する点は

$\left(\Large\begin{array}x\\y\end{array}\right) = t \left(\Large\begin{array}t\\t\end{array}\right)+(1-t)\left(\Large\begin{array}t-1\\1-t\end{array}\right)$

を整理して、

$\left(\Large\begin{array}x\\y\end{array}\right) = \left(\Large\begin{array}-1+2t\\1-2t+2t^2\end{array}\right)$

となります。

ここで注目すべきは、

$y=\Large\frac{1}{2}x^2+\frac{1}{2}$

が成立することです。２次ベジエ曲線は２次関数（放物線）だったのです。

同様に、直線の式を求めると、 $y = (2t - 1)x + 2t(1-t)$ となります。

放物線と直線が交わる点を求めるために、両者の y が等しいとすると、

$\Large\frac{1}{2}x^2+\frac{1}{2} = (2t - 1)x + 2t(1-t)$

$\Large(x - (2t-1))^2=0$

となります。

つまり、放物線と直線はただ１点でのみ交わる、ということです。これは、直線が放物線の接線であることを意味します。接線である以上、直線は放物線より上でもなければ下でもないことは自明です。

まとめ

なんだか数学の講義みたいになってしましたが、まとめるとこうなります。

２次ベジエ曲線
- ２次曲線（放物線）
- ２つの制御点が接点
CG の図
- 構成する直線は２次曲線の接線
- 構成する直線から浮かび上がる曲線は２次ベジエ曲線

次回は、Illustrator などのドローソフトでも用いられている「３次ベジエ曲線」を見ていきます。

おまけ

上の Flash のソースコードです。初めて Tweener を使ってみました。

package
{
    import flash.display.Sprite;
    import flash.geom.Point;
    import caurina.transitions.Tweener;
    
    public class BezierTest2 extends Sprite
    {
        private var SIZE:int = 300;
        private var t:Number = 0.0;
        private var p:Point = new Point();
        private var flag:Boolean = true;
        private var dot:Sprite;

        public function BezierTest2()
        {
            dot = new Sprite();
            dot.graphics.beginFill(0x000000);
            dot.graphics.drawCircle(0, 0, 3);
            dot.graphics.endFill();
            addChild(dot);

            addEventListener("enterFrame", function(event:*):void{drawLines()});
        }

        public function drawLines():void
        {
            graphics.clear();

            var pt1:Point = new Point(0, t * SIZE);
            var pt2:Point = new Point(t * SIZE, SIZE);
            var pt3:Point = getInnerPoint(pt1, pt2, t);

            dot.x = pt3.x; dot.y = pt3.y;

            graphics.lineStyle(1, 0xcccccc);
            graphics.moveTo(pt1.x, pt1.y);
            graphics.lineTo(pt2.x, pt2.y);

            var line:Sprite = new Sprite();
            line.graphics.lineStyle(1, 0x0099ff);
            line.graphics.moveTo(p.x, p.y);
            line.graphics.lineTo(pt3.x, pt3.y);
            addChildAt(line, 0);

            Tweener.addTween(line,
            {
                alpha: 0, 
                time: 3, 
                onComplete: function():void{removeChild(line);}
            });

            p = pt3;
            t = (flag ? t + 0.02 : t - 0.02);
            if(t >= 1.0 || t <= 0) flag = !flag;
        }

        private function getInnerPoint(p0:*, p1:*, t:Number):Point
        {
            return new Point(p0.x * (1 - t) + p1.x * t, p0.y * (1 - t) + p1.y * t);
        }
    }
}

てっく煮ブログ

ベジエ曲線の仕組み (2) - ２次ベジエ曲線を詳しく

ベジエ曲線の定義

前回の図と比較

証明１：力技

証明２：ちょっとエレガントに

まとめ

目次

おまけ